| University | Auckland University of Technology (AUT) |
| Subject | ENGE800/STAT 805 Engineering numerical Technique and Statically Analysis |
Introduction
The purpose of this asssessment is to assess your theoretical and computational skills on the materials covered in the second half of the course.
- Answer all questions Total mark: 100
- This project counts for 60% of your final grade.
- Justify your chosen solution method, providing appropriate reasoning where applicable.
- Upload your report on Canvas by the due date: Friday June 13, 2025 at 4:00pm.
Submission Requirements
- The assignment should be completed using R Markdown and should be compiled as a PDF document. (If you really have difficulty knitting a PDF, knit it as Word and then save as PDF.)
- Working steps, in terms of R code and output, should be embedded in relevant
places of the document (NOT as an appendix). - Submissions that contain large quantities of unnecessary or irrelevant code, output or text will be penalised
Stuck! Do not Know Assessment Answers?
Hire NZ Native Experts 24/7.
Late Assignments
Failure to submit the assignment on time without special consideration approved will result in a penalty in accordance with the faculty policy (i.e., 5% per day up to a maximum of 5 days). If you experience any extenuating circumstances that prevent timely submission, please apply for special consideration via Canvas.
Marking Criteria
Your work will be marked according to the correctness of techniques applied, explanations,
interpretations, and communication. A rubric is available on Canvas
Question 1: Nonlinear equations (10 marks)
Use Newton’s method to solve the equation
![]()
(a) Explain why the result seems unusual for Newton’s method (6 marks).
(b) What do you observe when you solve the equation with p0 = 5π and p0 = 10π?
(4 marks)
Question 2: Linear systems (20 marks)
Suppose the coal and steel industries form an open economy. Every $1 produced by the coal industry requires $0.15 of coal and $0.20 of steel. Every $1 produced by steel requires $0.25 of coal and $0.10 of steel. Suppose that there is an annual outside demand for $45 million of coal and $124 million of steel.
(a) How much should each industry produce to satisfy the demands? (10 marks)
(b) If the demand for coal decreases by $5 million per year while the demand for steel increases by $6 million per year, how should the coal and steel industries adjust their production? (10 marks)
Question 3: Intertpolation and approximation (15 marks)
Population censuses are generally conducted every 10 years, although in some countries, they are conducted every 5 years. Obtain the last six census population data for a country of your choice. Present the data in a table with one column for the Year and another column for the Population (in thousands of people).
(a) Use Lagrange interpolation to approximate the population for any three years in which a census was not conducted. (10 marks)
(b) How accurate do you think your estimated values are compared to the actual population in those years (if known)? (5 marks)
Buy Custom Assignment & Homework Solutions
Pay to NZ Native Writers | Cheap Cost & Plag Free
Question 4: Numerical differentiation and integration (25 marks)
(a) In a circuit with impressed voltage v(t) and inductance L, Kirchhoff’s first law gives the relationship
v(t) = L
di
dt + Ri
where R is the resistance in the circuit and i is the current. Suppose we measure the current for several values of t and obtain:
| t (seconds) | i (amperes) |
|---|---|
| 1.00 | 3.10 |
| 1.01 | 3.12 |
| 1.02 | 3.14 |
| 1.03 | 3.18 |
| 1.04 | 3.24 |
where the inductance L is a constant 0.98 henries, and the resistance is 0.142 ohms.
- Approximate the voltage v(t) when t = 1.00, 1.01, 1.02, 1.03, 1.04.
(10 marks) - Compute the actual errors and find error bounds. (5 marks)
(b) A particle of mass m moving through a fluid is subjected to a viscous resistance R,which is a function of the velocity v. The relationship between the resistance R, velocity v, and time t is given by the equation
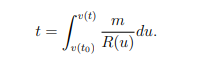
Suppose that R(V ) = −v
√
v for a particular fluid, where R is in newtons and v is
in metres/second. If m = 10 kg and v(0) = 10 m/s, approximate the time required for the particle to slow to v = 5 m/s. (10 marks)
Question 5: Initial value problem (20 marks)
The FitzHugh–Nagumo equations are a simplified version of the Hodgkin–Huxley model of neuronal activity. They capture the essential features of excitability and spike generation in neurons, using a two-variable system of ordinary differential equations (ODEs).
(a) Write down the standard equations of the FHN model with appropriate parameters
as initial value problem. (7 marks)
(b) Apply the Runge-Kutta Fourth-Order Method to approximate the solution with h = 0.5. (5 marks)
(c) What do you observe by increasing the step size to h = 1.5. Can we conclude that the system is a stiff system? (5 marks)
(d) Justify your answer in (c). (3 marks)
Question 6: Boundary value problem (10 marks)
In electronics, vacuum tubes with three internal elements (such as triodes) can exhibit nonlinear behaviour due to the complex interactions of voltage and current. One widely used model for the current flow through such a device is the Van der Pol equation:
y′′ − µ(y2 − 1)y′ + y = 0, µ > 0.
An engineer is analysing the transient behaviour of current y(t) in a vacuum tube
circuit is interested in the current at various time point given the following boundary conditions y(0) = 0, and y(2) = 1 with parameter µ = 0.5.
(a) Approximate the solution y(t), plot to visualise the behaviour of the solution.
(7 marks)
(b) Explore how the solution changes if µ is increased to a higher value (say µ = 2 or
µ = 3). (3 marks)
In quest for a professional assignment help?
Flexible rates compatible with everyone’s budget
If you are having difficulty completing your Numerical Methods Assignment, then no need to worry university assignment help service is here for you. Get expert-written essays at NZ Assignment Help and complete your assignment before the deadline. Don't delay, and contact us now to get high grades in your academics!
- 31866, 31867 & 31869 Portfolio of Evidence Assessment | Professional IQ College
- 31868 Providing Life, Disability and Health Insurance Services Assessment | NZQA
- 31865 Environment and Concepts Assessment 2026 | Professional IQ College
- 31861, 31862 & 31864 Investment Assets, Financial Instruments and Services Assessment Portfolio of Evidence
- 31863 Economic Solutions Assessment 2026 | Professional IQ College
- 31859 Investment Services Environment and Concepts Assessment | NZQA
- MAMC01801 Capabilities for Managers Assessment 2 Report | UOA
- EC731 Tiriti-Based Early Childhood Education Assessment | NZTC
- EDPROFST 762 Mentoring Professionals Assignment 2 2026 | UOA
- PTY608 Exercise Physiology & Rehabilitation Written Assignment 2026


